Note: Some programming experience, knowledge of the React JavaScript library, and an understanding of basic algebra and geometry are necessary to understand this post.
A few days ago while browsing Apple’s AppStore, I came across a new game that has raving reviews. It is called KAMI 2, and for a puzzle lover like myself, I was thrilled to find a new game to love. The visual design is beautiful (the designer in me is proud of whoever created it) and the animations are equally stunning. Some of the interactions of the app are a bit annoying (mainly navigation issues), but overall, the app is very well done and I immediately got hooked on the concept and gameplay.
The concept is simple: users are presented with an origami-inspired board of triangle-shaped tiles of various colors. The goal is to tap shapes (made of said triangles) of a particular color to flood fill that color section with one of the other colors on the board until the entire board is the same color. The intriguing thing is that you have to get the board to be one solid color in as few moves as possible (each level shows the number of moves required). The game is fun to play and I never tire of it (although I sometimes have to take a break to clear my head when one of the challenging levels frustrates me!). Solving a clever level feels so rewarding, which brings out the nerd in me!
There are two things that I find intriguing about this game. Remember that post I wrote about my iPhone/iPad game MentalBlocker? It has a game mode called Safe Zone that has blocks on a board that must be slid into designated safe zones in the least number of moves. Sound familiar? :) While playing KAMI 2, I started thinking: “How did the game developers go about writing an algorithm to get the fewest number of moves for a level, and how similar is that algorithm to what I did for MentalBlocker?” I also find it fascinating that they chose to use a triangle grid instead of the standard (and easier to implement) square grids that I am used to seeing and working with. I scratched my head for a long time trying to figure out how they set up the coordinate plane for this kind of grid. Officially intrigued, I started thinking about how I would go about creating a game like this. Let’s see how I did it!
Gameplay
The gameplay is pretty straight forward. There is a grid comprised of triangle tiles, each with a color property. Each level has a palette of two to five colors. The levels start off simple, with two colors and a couple shapes, and they develop into more complex boards with the addition of more colors and shapes to eliminate. Let’s start with a simple example, the game’s first level:
Grid Layout
Now that we understand the basic game dynamics, let’s analyze the grid layout. The game features an origami-inspired (the game name Kami is the Japanese word for ‘paper’) animation that flips the triangles over to show new colors during flood fill (as well as “folding” the entire board up upon level completion). From that perspective, I understand why the designers chose to use this grid layout (as an aside, it turns out that the first version of the game used squares, not triangles, to layout the grid). Triangles add an interesting dimension and a nice polish to the overall animation. The first thing I wondered was how they generated a grid of triangles like this. The triangles appear to be equilateral, and they are organized in a way that has each triangle pointing either left or right (like the shape of a rewind button and a play button, respectively). For experimental purposes, I decided to play around with some shapes to see how I could mathematically get such a grid. Using Illustrator, I created a square grid and changed some settings to transform it into an equilateral triangle grid. As it turns out, I had to use a bit of math.
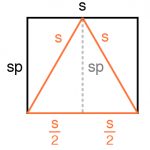
In the image above, we want to get the square in step 1 to transform into the two equilateral triangles in step 5. How do we do this, and what geometry is involved? Let’s review the math involved in creating an equilateral triangle grid. We start with the square (step 1), which we know has four equal sides. We inscribe a triangle inside of the square (created by the orange lines in step 2) such that the top vertex of the triangle bisects the top side of the square. The orange legs are thus the same length but are different from the length of a side of the square, so we have an isosceles triangle. However, we want the sides of this triangle each to be equal to a side of the square it inscribes (we’ll see why shortly).
Let’s see how we get from step 2 to step 3. Let’s call the length of the sides of the square s. As mentioned, our goal is to make the isosceles triangle shown in step 2 an equilateral one so that all of its sides equal s. To do this, we need to change the height of the square in step 2 so the square becomes a rectangle. Mathematically, this means we need to multiply the height of the square s by a specific factor (percentage) p so that the triangle’s sides all equal s and the square becomes a rectangle with height sp and width s. By then solving for p, we’ll have the fraction that we need to multiply s by in order to achieve this goal. Phrased as a question, we are asking: “If we want each side of the triangle to have length s, what must the new height of the square be?” Here’s how to solve for p using the Pythagorean theorem:
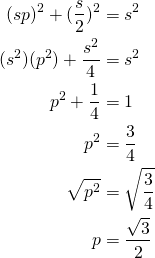
We see that in order to make the inscribed triangle equilateral, we need to multiply p by (√3)/2. This gives us the value we need in order to vertically scale the square down to (√3)/2 ≈ 86.602% of its original height. Now we have step 3 from figure (a) earlier. The reason we need our inscribed triangle to be equilateral is that it gives us one of the two equilateral triangles that we are transforming our original square into. You’ll see how we construct the second triangle in the next step.
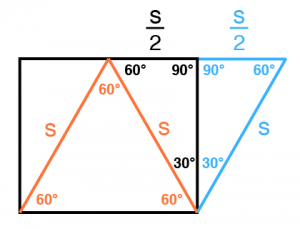
In step 4 of figure (a), we can derive the image shown to the left. We create a new triangle (shown in blue) as follows: add a line that starts from the bottom right corner of our black rectangle, making it parallel to the left leg of our orange equilateral triangle. Then extend a leg from the top right corner of the black rectangle so that it connects straight across to the line we just created. This second line is parallel to the bottom side of the black rectangle. Geometry ensures that since our orange triangle is equilateral, each of its three angles equals 60 degrees. Thus we can find the angles of the new blue triangle we just created. This shows that by adding this new blue triangle, we’ve constructed a second equilateral triangle, resulting in the figure below:
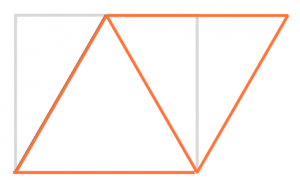
If we remove the black rectangle, we are left with the two orange triangles that you see above, and our original square-turned-oblong is left behind in the dust. Mathematically, what we essentially did is shear our oblong by 30 degrees (the bottom angle of the blue triangle shown earlier), and then we draw a line that bisects the resulting shape from its upper left corner down to its bottom right corner. Then, voila! We have our two equilateral triangles! :) To demonstrate this on a grid, here is a diagram that shows each step as done in Illustrator using our math from above:
The method that I used to create the equilateral triangle grid involves scaling, shearing, and bisecting the grid using the math explained above. First, I created a 6×6 square grid (step 1 above). Next, I compressed (scaled) the height of the grid to 86.602% of the original height (step 2). Then I sheared the grid (which is like pushing the top left corner of the grid to the right by a certain amount) by 30 degrees (step 3). Then I draw lines (shown in orange in step 4) to bisect each parallelogram into two equilateral triangles, resulting in the equilateral triangle grid shown in step 5. Note that the number of triangles generated will be twice the number of squares that we started with. In this example, our square grid of 36 squares transforms into an equilateral triangle grid with 72 triangles.
Note that our grid is comprised of triangles that point either up or down (try to see each triangle as an up or down arrow). If you look back at one of the screenshots from the actual game, you’ll notice that it has triangles that point left or right (try to picture each triangle as a rewind or play button). To achieve this orientation, we can simply rotate our grid by -30 degrees to achieve the below grid (you can also rotate by 30, 90, 150, etc. to achieve left-right orientation). Either orientation is suitable but I’ll explain why one is preferred over another shortly.
Grid Generation
Whew! Now that we have a comprehensive understanding of how triangle grids can be created from square grids, let’s get to the fun part: rendering such a grid in code! For the remainder of this analysis, I’ll be using Facebook’s React JavaScript library to explore the creation of this game. I chose this library because I’m currently learning it to do prototyping of some designs at work, so I get to practice using it in my spare time. Plus, in my book, nothing motivates learning programming more than game design and development! :)
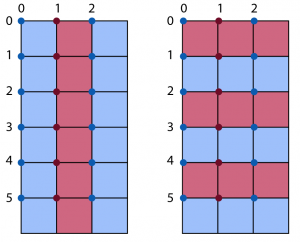
Let’s start by seeing how an up/down equilateral triangle grid is structured. Since our grid will be rendered in a 2-dimensional pixel-based environment on a smart device or computer, we need to ensure that we can use x and y coordinates when generating our grid on the screen. In a square grid, it is easy to see which row and column a square is in. With triangle grids, it can be a little trickier.
Let’s look at the above example of a square grid, with the origin (0,0) anchored to the top left to reflect how SVG’s are rendered in HTML. This will be our point of origin for the rest of this post. In the image shown above, we have a grid with six rows and three columns. It is easy to see exactly which row and column each square belongs to (by using alternating red and blue; the columns are shown on the left and rows on the right). We can pick any corner point of a square as the point where the placement of a square (where it is anchored) begins. In this example, I chose the top left corner of each square as the vertex that corresponds to the row and column where the square resides. The blue and red dots represent these starting positions, and each starting position represents a (row, column) point on the grid.
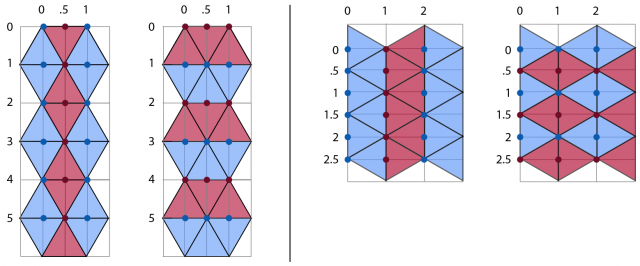
Let’s do the same for two versions triangle grid, one with triangles that point up/down, and another with triangles that point left/right:
It is now much easier to see the columns and rows, which are easily distinguishable with alternating blue and red colors. Before we reason about what exactly is going on here with the axes, let’s look at the layout differences between an up/down and a left/right triangle grid. While sketching out ideas for how to implement the grid in code, I started wondering if there is a benefit to having the triangles point up and down versus left and right. Looking at the orientations, you may notice something interesting: both orientations have six rows and three columns, yet the direction of the triangles gives us very different layout sizes. In the up/down orientation, the grid grows taller than its left/right counterpart. By contrast, the left/right orientation grows wider than its up/down counterpart. This is because the triangles are anchored every half-width of a triangle in the columns of the up/down orientation, yet staggered every half-width of a triangle in the rows of the left/right orientation row index (this is why the appropriate axis for each orientation is half-stepped; I’ll explain more about this shortly). This is crucial for grids that have a greater number of rows than columns (which works out perfectly for mobile screen portrait orientations). Even though both grid orientations have the same number of triangles, the surface area of the up/down grid will always be larger than that of a left/right grid when the number of rows is greater than the number of columns. For this reason, it makes more sense to generate game levels using the left/right orientation to maximize the number of triangles that can fit on the screen.
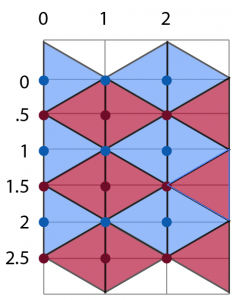
Now that we know which orientation to work with, let’s discuss an important aspect of the left/right grid. Each row height equals the length of an edge of a triangle, which is its width, and each column width is the height of a triangle. Every row in the grid includes all of some triangles and only half of the other triangles. This staggering means that we need to start the placement of every triangle in increments of half a row, which is why the row axis increments by 0.5 instead of 1. This staggering by half is crucial to determining which row a triangle belongs to. We’ll also need a way to ensure that when we draw our grid on the screen, each triangle is positioned properly (we need to know whether a triangle points left versus right). Otherwise, the negative space around each triangle will show if we space each triangle out according to only multiples of the rows and columns. The reason we don’t have this problem with squares is because the surface area of the XY-plane directly corresponds to the area that can be covered by squares. With triangles, we need to offset the positions of every other triangle in a row by half the length of a triangle’s side,
The reason we don’t have this problem with squares is because the surface area of the XY-plane directly corresponds to the area that can be covered by squares. With triangles, we need to offset the positions of every other triangle in a row by half the length of a triangle’s side, and we need to flip every other triangle left or right to ensure that we have properly offset and fit each triangle together with no gaps. This sounds tricky, but the alternating blue and red rows and columns in the previous image should help make it clear. Instead of anchoring the position of each triangle to the top left corner of a given cell (like we did with the square grid), we instead use a point located in the left middle, since no matter which orientation a triangle is in (left or right), the point will always be on the triangle (either as a vertex of a triangle, or a point that bisects a side of a triangle). This is conveyed by the small blue and red circles in the image: each circle corresponds to the triangle directly to the right of it.
In order to figure out where on the grid a particular triangle goes, we need to decide whether it should point left or right, and also whether it starts at an integer row number or a fraction row number. Let’s see how this works. If we create a 2D array of all the triangles (passed in React to a component class named Board), each triangle instance (represented in React as a component class named Triangle) will have a row and column specified (along with its color and other properties as well as states). All triangles in the grid will have the same side lengths. The column number times the height of the triangle corresponds to the x-coordinate of the leftmost point of a given triangle. The y-coordinate is slightly trickier to calculate: since the triangles start every half-width of a triangle, we need to calculate the y-coordinate by using half steps for the row number instead of full steps. Thus when creating the grid, each row should start at zero and increment by .5 until the desired number of rows is created. In our example, there are six rows, so the row numbers provided are 0, .5, 1, 1.5, 2, and 2.5 (as shown in the image).
In my React version of the game, a function is used to get the coordinates for every triangle on the board. An array that contains all the triangle data is passed from a Game component to the Board component, and the number of rows and columns on the board is determined from this array. The board receives this data and generates a Triangle component for each required triangle on the board. In the Triangle class, there is a function that gets the coordinates for a triangle using the following JavaScript function. The coordinates are then stored in each Triangle instance’s SVG data in the render method, which allows the triangles to appear on the screen in their proper locations.
// getPointsForTriangle: Returns the SVG triangle vertices in an array of format: [bottom: 0, top: 0, middle: 0]
// Note that SVG's coordinate plane has (0,0) in the top left corner.
// PARAMETERS: the row and column of the triangle
// Triangles point left or right. Row should be a float (for triangle offset) col is an integer
1. function getPointsForTriangle(row, col) {
2. let width = this.getSize().width; // width of triangle
3. let height = this.getSize().height; // height of triangle, which is the column width
4. let x = col * height; // x starts at leftmost point of triangle
5. let y = (row + 0.5) * width; // y starts halfway down the width of triangle
// See if this triangle should be drawn pointing left or right
6. const wholeRow = Number.isInteger(row); // bool
7. let pointsLeft = false; // bool
8. if (col % 2 == 0) {
9. pointsLeft = !wholeRow; // Even column
10. } else {
11. pointsLeft = wholeRow; // Odd column
12. }
13. var points;
// Draw the triangle.
14. if (pointsLeft) { // vertex points left (like rewind button)
15. points = {
16. bottom: { x: x + height, y: y + width/2 },
17. middle: { x: x, y: y },
18. top: { x: x + height, y: y - width/2 }
19. };
20. } else { // vertex points right (like play button)
21. points = {
22. bottom: { x: x, y: y - width/2 },
23. middle: { x: x + height, y: y },
24. top: { x: x, y: y + width/2 }
25. };
26. }
27. return points;
28. }
Let’s analyze what’s happening here line by line. In lines 2-5, we get the width and height of the triangle and then calculate the row and column position based on the method I just described. Notice that the x and y positions are set so that their coordinates give us the middle of the left-most side of the triangle (this corresponds to the circles shown in the image below). This middle-left point corresponds to the anchor point that will be where our three vertices are relative to. Things get interesting in lines 6-12. We need to determine whether the triangle points left or right. To see how this is done, look at the image below:
Notice that triangles that are in a whole number row and an even number column point right. Triangles that are in a whole number row and an odd number column point left. Conversely, for triangles that are in a fraction row, if they are in an even number column, they point left. Otherwise, they point right. Line 6 checks to see whether the row is an integer or a fraction and stores the result. Then we check if the column is even or odd and determine whether the triangle should point left or right based on whether the row is an integer or not.
Next, we determine the actual point values. Recalling that the point (x,y) corresponds to a triangle’s middle-leftmost point, we can use this point to determine the vertices of each triangle. If the triangle points left, then the coordinate (x, y) is already on the triangle’s leftmost vertex, so we simply set those two points for the middle coordinate (note that we return the three vertices in an object that stores three objects: bottom, top, and middle, each of which store the x and y values). Since we know this triangle points left, we can simply move to the right by one column width (recalling that the width of each column equals the height of the triangle) and then up or down by half the triangle’s width to get the top and bottom vertices, respectively. On the flip side (pun intended, ha!), if the triangle points right, then the starting coordinate (x, y) is in the middle of the triangle’s left edge. We can move up half of the triangle’s width to get the top point, move down half of its width to get the bottom point, and move right by its height to get the middle point (all moves relative to the starting point (x, y)). Easy enough!
Once we have all the coordinates for the vertices, we update the triangle’s coordinates state and then return the points object. And just like that, we can generate the entire grid! This is a screen shot of what the grid looks like in my game so far, with the same size and number of triangles as the iPhone game, but with swapped row and column numbers so I can save vertical space on the page:

Beautiful isn’t it?! :) I made some modifications to my CSS so that the main SVG wrapper has a radial background and the stroke of the triangles are thin and dark. I also randomized the opacity of each triangle so it looks like each one has more of the look and feel of the actual game.
Flood Filling
Graph Traversal Algorithms + Animations
Next up, we need a way to flood fill areas of the board. To do this, we need to consider two things: finding the neighbors of a triangle to change the color of, and finding out which conditions are necessary for the flood fill to continue. In order for two triangles to be neighbors, they must share an edge, which means they share two vertices. If they share only one vertex, then they are only touching at one point and thus have no shared edges. If they share zero vertices, then they aren’t touching each other at all. Each triangle in our grid thus has at most three valid neighbors.
When a triangle is clicked, we want to change its color (if applicable, since the triangle may already be the desired color) and then change the color of its neighbors, and its neighbors’ neighbors, and so on, spreading the color around the board until we find either an edge of the board or a color other than the originally clicked triangle’s color. To flood fill an area with a new color, we can use a graph traversal algorithm. Think of the grid as a graph that has triangles for vertices and edges between all valid neighbors. For the traversal, the source node will be the clicked triangle. The goal is to traverse the graph until no more valid triangles are left to explore. We have several options to do this, and we’ll consider two popular choices. Let’s start with Depth First Search.
Our general approach to flood filling the board will be as follows:
- See if the color of the clicked triangle is already the flood fill color. If the colors are the same, then the clicked triangle doesn’t need to be changed and we’re done.
- If the clicked triangle’s color isn’t the same as the flood fill color, then change it to the new color.
- Get the clicked triangle’s neighbors, seeing which are both in bounds and the same color as the triangle that was originally clicked on. These neighbors will be flood filled with the new color, and then their neighbors are each checked, and so on until no triangles are left to consider.
At this point in my game, I’ve added a way for the player to select a color. When the user changes her selected flood fill color and clicks on a triangle on the board, it will determine what to do next based on the steps above. Depth First Search works by “pushing down” a branch until it can’t go down any further before changing direction: it goes completely down one branch before backtracking to explore another branch. We can use a stack data structure to achieve this, or we can utilize recursion to create the stack for us with repeated function calls. Both will achieve the same result. Let’s take a look at both versions of the code, starting with the recursive version.
// floodFillDFSrecursive: Recursively flood fill the board. //Note that SVG's coordinate plane has (0,0) in the top left corner.// PARAMETERS: // clickedTriangle, Object: {row: 1, col: 1, color: "#C44368", pointsLeft: false} // trianglesClone: an array of triangles in the same format as the first parameter. // This represents a copy of the original game board that will be updated with the new // changes and stored in a history state to keep track of the user's moves (so she can undo moves later) // TrianglesToUpdate: an array of triangles in the same format as the first parameter. // It is used to keep track of which triangles changed for animation purposes. 1. floodFillDFSrecursive(clickedTriangle, trianglesClone, trianglesToUpdate) { 2. const newColor = this.state.currentColor; // current flood fill color 3. const origColor = clickedTriangle.color; 4. const x = clickedTriangle.row; 5. const y = clickedTriangle.col; 6. const pointsLeft = clickedTriangle.pointsLeft; 7. const key = this.getTriangleKey(x, y); // this function computes the index of the triangle // based on the board's number of columns // ensure this triangle is within the board's bounds and is the originally clicked color: 8. if (this.isInBounds(x, y) && trianglesClone[key].color === origColor) { 9. trianglesClone[key].color = newColor; // fill the cell 10. trianglesToUpdate.push(trianglesClone[key]); // 4 possible recursive calls to check left, bottom, right, and top neighbors. // Only up to 3 will work at a time since each neighbor has at most 3 neighbors 11. if (!pointsLeft) { // if triangle points right, then it has a left neighbor 12. this.floodFillDFSrecursive({ // pass in the new parameters 13. key: key, 14. row: x, 15. col: y - 1, // left neighbor 16. color: origColor, 17. pointsLeft: !pointsLeft // because every triangle's neighbor always points the opposite direction 18. }, trianglesClone, trianglesToUpdate); 19. } 20. this.floodFillDFSrecursive({ 21. key: key, 22. row: x + 1, // bottom neighbor 23. col: y, 24. color: origColor, 25. pointsLeft: !pointsLeft 26. }, trianglesClone, trianglesToUpdate); 27. if (pointsLeft) { // if triangle points left, then it has a right neighbor 28. this.floodFillDFSrecursive({ 29. key: key, 30. row: x, 31. col: y + 1, // right neighbor 32. color: origColor, 33. pointsLeft: !pointsLeft 34. }, trianglesClone, trianglesToUpdate); 35. } 36. this.floodFillDFSrecursive({ 37. key: key, 38. row: x - 1, // top neighbor 39. col: y, 40. color: origColor, 41. pointsLeft: !pointsLeft 42. }, trianglesClone, trianglesToUpdate); 43. } 44. }
Hopefully, my comments make this algorithm clear. A recursive call is popped off the stack when each of the four possible recursive calls in the function no longer having valid triangles to recurse on, either because a triangle is out of bounds, or it isn’t the originally clicked triangle’s color.
Note that for the purposes of the flood fill, it doesn’t matter which order we list the recursive calls. It does impact the order in which triangles are recolored, though. Since I want to animate the flood fill triangle by triangle, it is interesting to see how the order in which I make the recursive calls changes the animation of triangles as they are recolored. Using the order of left, bottom, right, and top as shown above, here is an example of the flood fill in action, using a slow animation so you can follow what is happening:
Note that the recursive calls will attempt to animate the triangles in the same order: each time a triangle is recursed, it will try to recurse its left neighbor if that is a valid neighbor, if not, it will recurse on its bottom neighbor, and so on, and then in the next call that is made on a triangle, it will repeat the same process in that order, recursing on whichever of the four possible neighbor locations is next validated. This process repeats for each triangle until the entire valid region is flood filled.
Next, let’s look at the non-recursive version of Depth First Search. This algorithm uses an array as a stack to non-recursively flood fill an area on the board.
// floodFillDFSstack: uses an array as stack to implement Depth First Search.
// PARAMETERS: same as recursive version.
1. floodFillDFSstack(clickedTriangle, trianglesClone, trianglesToUpdate) {
2. let visitedTriangles = new Set();
3. var stack = [clickedTriangle]; // this is an array that will serve as the stack
4. while (stack.length) {
5. let currentTriangle = stack.pop();
6. const key = this.getTriangleKey(currentTriangle.row, currentTriangle.col);
7. trianglesClone[key].color = this.state.currentColor; // update color in board array
// getNeighborsForTriangle() is straightforward; it gets valid neighbors similar to
// what we did in the recursive version and returns them in an array
// The order in which the neighbors are delivered is top, right, bottom, left.
8. let neighbors = this.getNeighborsForTriangle(currentTriangle, trianglesClone, trianglesToUpdate);
9. currentTriangle.id = key; // set unique identifier so we can see if we've visited a triangle already
10. if (!visitedTriangles.has(currentTriangle.id)) {
// if we haven't seen this triangle before, mark it as visited, update its color,
// and add it to array of updated triangles. Stack may contain same triangle twice,
// so we need to color the popped triangle only if it is not visited.
11. visitedTriangles.add(currentTriangle.id);
12. currentTriangle.color = this.state.currentColor;
13. trianglesToUpdate.push(currentTriangle);
14. }
15. neighbors.forEach((neighbor) => {
16. neighbor.id = this.getTriangleKey(neighbor.row, neighbor.col);
17. if (!visitedTriangles.has(neighbor.id)) { // make sure we haven't visited this triangle already
18. stack.push(neighbor);
19. }
20. });
21. }
22. }
The getNeighborsForTriangle method generates neighbors in the following order: top, right, bottom, left (skipping east or west depending on whether a triangle points left or right). Notice that this algorithm fills in triangles in the reverse order in which neighbors are generated, so it will prioritize left, bottom, right, and top. This will give us the same animation pattern as the recursive version shown above! This shows that the algorithm works the same exact way, using two very different implementations.
Look again at our Depth First Search animation. It is cool to see how the board is colored in, but wouldn’t it look more polished if the color radiated out from the clicked point, growing outward like a blooming flower? Breadth First Search can achieve exactly that behavior. Since it uses a queue to store the triangles, the triangles are re-colored one level at a time. Let’s look at the algorithm, which uses an array that behaves like a queue by using JavaScript’s shift() function on the array to dequeue each triangle.
// floodFillBFSqueue: uses a queue (an array that uses shift() to dequeue and push() to enqueue)
// to implement Breadth First Search.
// PARAMETERS: Same as Depth First Search functions.
1. floodFillBFSqueue(clickedTriangle, trianglesClone, trianglesToUpdate) {
2. clickedTriangle.id = this.getTriangleKey(clickedTriangle.row, clickedTriangle.col);
3. let visitedTriangles = new Set();
4. visitedTriangles.add(clickedTriangle.id);
5. var queue = [clickedTriangle]; // this is an array that will serve as the stack
6. while (queue.length) {
7. let currentTriangle = queue.shift();
8. trianglesClone[currentTriangle.id].color = this.state.currentColor;
9. let neighbors = this.getNeighborsForTriangle(currentTriangle, trianglesClone, trianglesToUpdate);
10. currentTriangle.color = this.state.currentColor;
11. trianglesToUpdate.push(currentTriangle);
12. neighbors.forEach((neighbor) => {
13. neighbor.id = this.getTriangleKey(neighbor.row, neighbor.col);;
14. if (!visitedTriangles.has(neighbor.id)) {
15. visitedTriangles.add(neighbor.id);
16. queue.push(neighbor);
17. }
18. });
19. }
20. }Notice that this algorithm fills in triangles in the order in which neighbors are generated in the getNeighborsForTriangle method: top, right, bottom, left (skipping east or west depending on whether a triangle points left or right). Here is the animation:
Smooth, huh? Now let’s look at some real game levels! This is a level from the app on the left, next to an animation of my version for comparison. This level is solved in the least number of moves.
Finding solutions to a level
Edge contraction + a Breadth/Best First Search game tree
Finding solutions to a level is probably the most challenging part of this experiment for me. In MentalBlocker, it was simple enough to generate a game tree in which I use Breadth First Search to find all the possible moves (finding all the placements of blocks after sliding each block in each possible way). This gives me a game tree where each level is comprised of all the moves that are possible from the level before. This was achievable in a reasonable amount of time because there were only a handful of blocks on the board, and the rules by which they are allowed to move across the board gave each block only up to four possible moves per turn. In KAMI 2, every triangle is its own entity. If we check each triangle one by one and see what area can be flood filled, we’d end up in cases where more than one triangle results in the same flood fill, which would generate more game states than necessary. Instead, we need a way to only consider each colored section on the board as its own entity. Put another way: if we construct a graph of the board and then collapse each section of the board that can be flood filled with a color (let’s call these sections color shapes) into a single vertex, we will end up with a k-coloring of the board, where k represents the number of colors used in the level. (K-coloring a graph uses k colors to color the vertices of the graph in such a way that no two adjacent vertices have the same color.) It is also worth noting that optimally solving this type of problem is NP-hard. This simplified board can be used to generate our game tree. Let’s see how this works!
First, let’s represent our graph in code using an adjacency list that is represented by an array. Each index in the array will correspond to the index of a node in the graph (as in a triangle on the board), and the value at that index will be an array of the indices of nodes that are adjacent to the node represented by that index. For example, if node 0 connects to nodes 1 and 2, then the first element of the adjacency list will correspond to node 0, and it will contain the array [1, 2], to represent the edges that node 0 has to its adjacent nodes. The adjacency list thus has |V| arrays: one array of adjacent nodes per node.
Next, we need a way to traverse our grid in a way that allows us to combine valid neighbor nodes of the same color together into a single node, repeating this process of contracting edges between alike nodes until we have done this on the whole graph. Using this edge contraction approach to simplify a game level’s graph will be the first step towards solving levels. It greatly reduces the number of possible moves that can be made in our game tree. Let’s show an example of how this works.
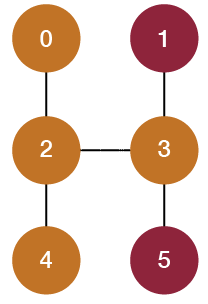
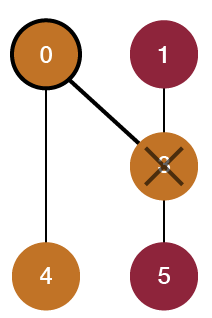
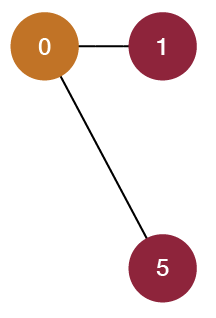
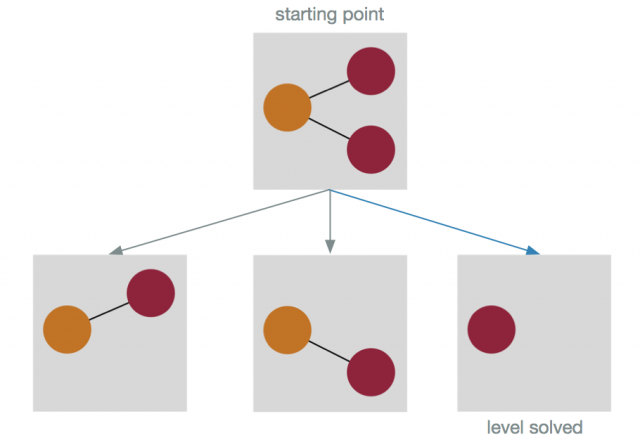
Let’s consider this tiny board as an example to illustrate the concept of contracting edges. Can you see how many color shapes are on this level (how many areas can be flood filled)? There are three: the connected yellow area, and the two red triangles that are disconnected from each other. Remember this number! It will be relevant later. To start, first let’s visualize this level as an actual graph, where each triangle is connected to its valid neighbors (regardless of color) by an edge. We’d end up with this:
This shows the graph version of the level, with each node numbered with its key, starting at 0 and incrementing left to right, row by row (we also generate keys for the triangles in the same way; remember that the point of origin is located at the top left of the level/graph because that is how SVG elements are rendered). Remember that two triangles are neighbors only if they share an edge. Thus nodes 0 and 1, for example, are not neighbors, so there is no edge drawn between them in the graph.
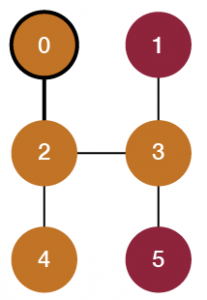
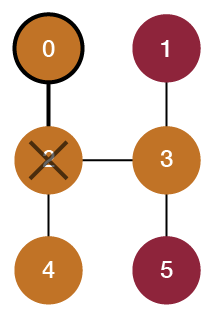
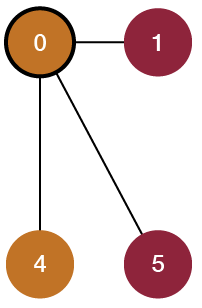
Now that we have our graph, it’s time to simplify it. First, we will look at node 0 at location (0, 0). We’ll consider this node’s neighbors (adjacent nodes, regardless of color), one by one. This node has only one neighbor: node 2. For each neighbor we see, if its color is the same as the considered node’s color, then we will delete the neighbor and then add edges from the considered node to all nodes that were adjacent to the deleted neighbor. This will simplify the graph by removing a duplicate color node while maintaining that the originally considered node will still be able to reach whichever nodes the deleted neighbor was connected to. If a neighbor is a different color from the considered node, then we ignore it and move on (since we do not want to delete nodes of different colors that we need to consider later). We repeat this process for every neighbor until we’ve checked them all, at which point we then consider the next node in the graph (reading the nodes row by row from left to right). Let’s show what happens when we check the neighbors using this method.
0 -> 2
1 -> 3
2 -> 0, 3, 4
3 -> 1, 2, 5
4 -> 2
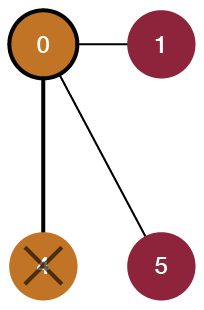
5 -> 30 -> 2 3, 4
1 -> 3
2 -> 0, 3, 4
3 -> 1, 2, 5, 0
4 -> 2 0
5 -> 30 -> 3, 4
1 -> 3
3 -> 1, 5, 0
4 -> 0
5 -> 30 -> 3 4, 1, 5
1 -> 3 0
3 -> 1, 5, 0
4 -> 0
5 -> 3 00 -> 4, 1, 5
1 -> 0
4 -> 0
5 -> 00 -> 4 1, 5
1 -> 0
4 -> 0
5 -> 00 -> 1, 5
1 -> 0
5 -> 00 -> 1, 5
1 -> 0
5 -> 00 -> 1, 5
1 -> 0
5 -> 00 -> 1, 5
1 -> 0
5 -> 00 -> 1, 5
1 -> 0
5 -> 00 -> 1, 5
1 -> 0
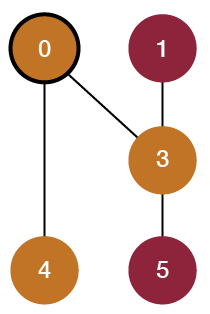
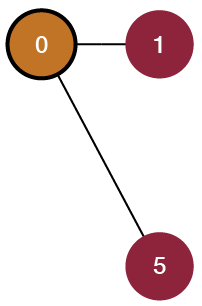
5 -> 0This shows that when we are done simplifying our graph, the remaining number of vertices represent the number of color shapes on the original level. This shows that we’ve simplified the board into the smallest number of vertices. In this example, the remaining vertices are 0, 1, and 5. Each vertex represents a valid location on the board that is the same color and is part of one color shape. In this case, the board has two colors, and our simplified graph is a 2-coloring.
Here is the final sequence of events so you can see it all inline:
Note that although we now have two representations of the board (one in an array and one in a graph), this approach still works best for our use cases. The array is used for quick access to triangle elements when updating and rendering the level. The graph is used to contract the edges into the simplest form of the board that is comprised of one node per color shape on the level, which allows us to use this simplified graph to find a solution for the level. Thus having both structures is beneficial.
Now that we’ve modeled the way we can simplify a graph, let’s look at the algorithms that allow us to do this. The graph data structure is pretty simple; it is a graph object that uses arrays to store the vertices and edges. It also has a copy of the board’s array of triangles so we can check the color of each vertex in the contracting stage. Our graph has methods to add and remove vertices and edges. Here is the JavaScript algorithm for pruning the original graph into its k-colored graph:
// pruneGraph: goes through vertices, deleting same-colored ones and contracting relevant edges
1. Graph.prototype.pruneGraph = function() {
2. var v = 0; // v is the key of the vertex we are checking in the graph
3. while (this.edges[v] != undefined) { // while we still have a vertex to check:
4. var e = 0;
// e is the index of a vertex that has an edge to the current vertex.
// We'll increment this only when we reach an edge that can't be contracted,
// which will ignore and skip over that vertex and go to the next vertex.
// Otherwise, this vertex is removed and its edges are contracted, which
// then replaces the vertex at the current index with the next edge to contract.
5. while (this.edges[v][e] != undefined) { // while we have a neighbor to consider:
6. if (!this.contractEdge(v, this.edges[v][e])) {
7. ++e; // nothing to contract; look at next edge.
8. }
9. }
10. ++v; // we reach here only when done considering the current vertex and ready to consider the next.
11. }
12. }Because of the way we check the vertices on the board in this algorithm, the final simplified board will contain nodes that were considered the first time a new color shape was found (its top leftmost triangle). This is because we check the nodes in the graph from the first to the last row and from left to right, so once we’ve found a triangle with a new color that represents a new color shape, every neighbor node that matches the new color will be deleted and its edges are contracted into the first node of that color shape. You can verify this yourself with the example shown.
The contractEdge() JavaScript function works by deleting and then contracting nodes if two nodes that share an edge have the same color. Here’s the code:
// contractEdge: Compares two nodes: if the second node is the same color as the first node,
// remove it and contract its edges into the first node.
// Returns true if a contraction is possible; returns false otherwise.
// PARAMETERS: v1 and v2, the nodes to compare.
1. Graph.prototype.contractEdge = function(v1, v2) {
2. var contracted = false;
3. if (v1 != v2 && this.vertexColors[v1].color === this.vertexColors[v2].color) {
// colors are the same, so pruning/contracting is possible
4. var v2edges = new Array(); // make copy of v2's edges so we can merge them with v1 after deleting v2
5. for (var j = 0; j < this.edges[v2].length; j++) {
6. v2edges[j] = this.edges[v2][j];
7. }
8. this.removeVertex(v2); // node not needed since it is the same color as v1, so delete it
9. contracted = true;
10. for (var i = 0; i < v2edges.length; i++) {
11. if (v1 != v2edges[i]) { // don't add edges from a node to itself
12. this.addEdge(v1, v2edges[i]); // add the edge to v1 (if it doesn't already exist)
13. }
14. } // otherwise, v1 and v2 are either not the same color, or they are the same, so don't prune/contract
15. }
16. return contracted;
17. }
We are now ready to use this simplified graph to generate a game tree. The game tree’s root node is the starting state of the board. Every possible move from any given game state will be represented as a child of that game state. A possible move consists of picking a color from the palette and then selecting a color shape to flood fill. Thus the number of possible moves and thus the number of children a game state can have is equal to (number of color shapes)*(number of colors in the palette – 1). We subtract 1 from the number of colors because filling in a color shape with its own color does nothing. To stop our graph from generating levels infinitely, we will prune branches of the tree by stopping further development of a branch when we either find a solution or see a game state we’ve seen earlier in the tree (since seeing it earlier means we got there earlier with the same or fewer number of moves than the current game state got us there). We will generate the game tree via Breadth First Search, searching for the shortest solution along the way. As explained in my MentalBlocker post, Breadth First search guarantees that the first time we find a solution will be the best solution, where the least possible number of moves needed to solve the level will be equal to the number of the level of the tree that the solution was found on.
Here’s the game tree for our sample board:
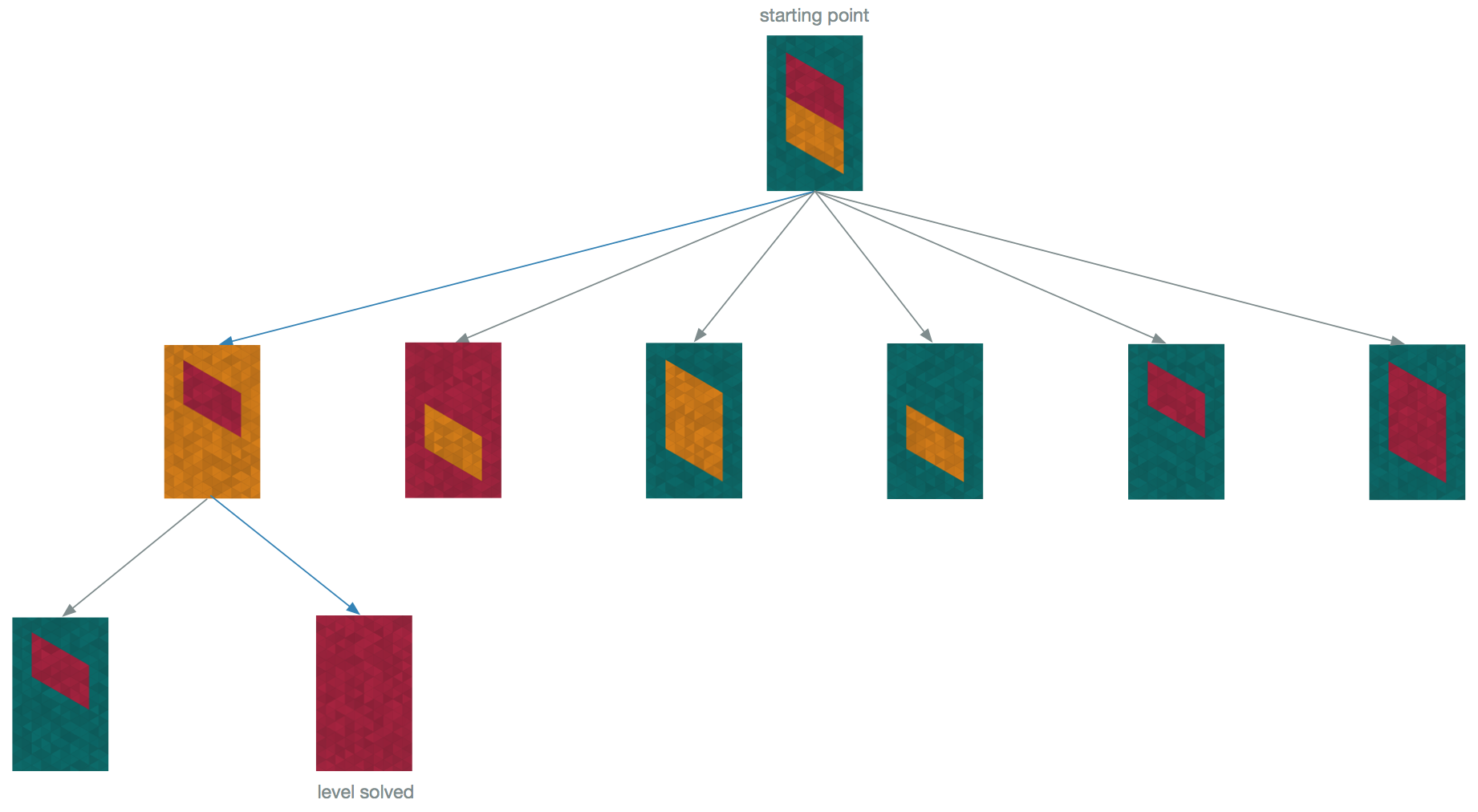
Since this board can be solved in one move, the tree only has two levels: level 0 (the root) and level 1. The solution was found on level 1 in the last game state on that level where the entire board is red (recall that a board is solved when it is all one color). Since this is the first solution found, this is the best solution and we can stop generating the tree. When we write our solver algorithm, we will generate this game tree using the simplified graph, and every time we change the color of a node, we then run pruneGraph() on the graph again to further simplify it and get the new game state. After each move, we simply check if the simplified graph has one vertex, which would mean it represents one color state that fills the entire board, which in turn means we have a solved level. Conceptually, that game tree for the graph version of the board would look like this:
Let’s look at a more intricate example on a new board:
This level is solved in two moves. Notice how on level 1 (the second level), the tree contains all the possible moves that can be made from the starting root node: since there are three colors, each color shape can be changed to one of the other two colors. Since there are three color shapes on the root level, there are 3*2 = 6 possible first moves, as shown on this level.
Now we can write our algorithm for generating the game tree. Here is the JavaScript function:
// solveBFS: Generates a game tree using Breadth First Search to find the best solution.
// PARAMETERS: colors, an array of colors where each index corresponds to a vertex in the graph.
// This is used to determine what colors a particular vertex can be changed to.
1. Graph.prototype.solveBFS = function(colors) {
2. this.pruneGraph(); // simplify graph before soliving.
3. this.level = 0; // store the BFS tree level with each game state. This is the root node.
// if only one game state is present, then board is solved! This is only true is passed in board is already one color.
4. if (this.size() === 1) {
5. printSolution(this);
6. return this.level;
7. }
8. var queue = [this]; // enqueue the current graph in a new queue
9. var visited = new Set();
10. visited.add(getHash(this));
11. while (queue.length) {
12. var poppedGraph = queue.shift();
13. for (var v = 0; v < poppedGraph.size(); v++) { // for each vertex
14. for (var c = 0; c < colors.length; c++) { // for each color
15. var poppedVertex = poppedGraph.vertices[v];
16. if (colors[c] !== poppedGraph.vertexColors[poppedVertex].color) {
// if this vertex's color is a different color than c, then create a new game state:
17. var graphCopy = new Graph(poppedGraph.vertexColors, poppedGraph);
18. graphCopy.vertexColors[graphCopy.vertices[v]].color = colors[c]; // change the color in the new game state
19. graphCopy.pruneGraph(); // simplify the game state's graph since we changed the color of a node
20. graphCopy.level = poppedGraph.level + 1; // set BFS tree level
21. graphCopy.parent = poppedGraph; // set parent so we can backtrack from this branch to root node to trace solution path
22. graphCopy.changeMade = 'make color shape at triangle ' + poppedVertex + ' ' + colors[c]; // used to track solution when we find one
23. if (graphCopy.size() === 1) { // if there is only one node left, then board solved!
24. printSolution(graphCopy);
25. return graphCopy.level;
26. } else if (!visited.has(getHash(graphCopy))) { // only enqueue unique game states
27. visited.add(getHash(graphCopy));
28. queue.push(graphCopy);
29. } // otherwise, a duplicate game state was found.
30. }
31. }
32. }
33. }
// Prints the steps required to solve the level.
34. function printSolution(graph) {
35. console.log('fewest number of moves needed to solve level is ' + graph.level + ':');
36. var changesMade = [];
37. while (graph.parent) {
38. changesMade.push(graph.changeMade);
39. graph = graph.parent; // update graph to consider higher in the game tree
40. }
// the steps that are made towards the solution start at the last move and go backwards toward first move,
// so print steps in reverse so we see them in the right order:
41. while (changesMade.length) {
42. console.log(changesMade.pop());
43. }
44. }
45. function getHash(graph) { // used to generate the unique string that identifies each game state
46. var hash = '';
47. for (var v = 0; v < graph.size(); v++) {
48. hash += graph.vertices[v] + ':' + graph.vertexColors[graph.vertices[v]].color + '|';
49. }
50. return hash;
51. }
52. return -1; // no solution found
53. };This code will take the graph version of a game board, prune it, and then run Breadth First Search on it by generating a game tree that searches for a solution. Once a solution is found, the path to the solution is printed out and the least number of moves required to solve the board is returned. And just like that, after all this hard work, we can now solve any level! Mission accomplished! Note, however, that this is not an optimal algorithm. While it only takes a fraction of a second to find a solution on game levels with just a handful of color shapes, it takes much longer to run on more complex boards. Our game tree has a branching factor b no larger than (number of colors – 1)(number of color shapes), so as an upper bound on the worst case scenario, our tree will grow exponentially very quickly on boards with a lot of game states, which will easily exhaust memory in a matter of minutes (I tried running my algorithm on a board with 64 color shapes, shown below; my computer ran out of memory after few minutes). So if a particular board can be solved on some level d, then the time/space complexity would be equal to the total number of nodes, which equals 1 + b + b^2 + b^3 + … + b^d = O(b^d). Yikes!
To remedy this, I started thinking about ways to improve the algorithm. Let’s look at the problem using the board shown above, which has a whopping 64 color shapes! It also uses four colors. In this example, the top left and bottom right corners of the board are missing; I updated my code to allow me to specify which triangles are not part of the board, so I can match the boards from the app exactly as they appear. This particular level is the sixth puzzle on the twelveth page of the Journey puzzles. Using Breadth First Search on this board would generate a game tree that has at most (64*3)^L nodes per level, where L is the level of the tree. How can we improve this algorithm to find an optimal solution in a reasonable amount of time?
I started wondering if there is a heuristic we can use to speed up the decision about which color shapes to change at every move, instead of brute-force checking every possible game state each step of the way. As I played the game, I noticed a strategy develop that I started using on every single level, and the strategy greatly increased the speed at which I solved each level. The idea is this: absorbing colors (merging as many color shapes of the same color in the fewest moves possible) seems to be a way to quickly solve a level. For any given level, there are a certain number of color shapes of a particular color. I try to eliminate all of one color in one move if possible. If I can’t do it in one move, then I try to do it in two moves, which usually means that I need to change the color of another shape in order to connect all the color shapes of a particular color. I keep doing this until I connect and eliminate one color from the entire board. The goal should be to have a way to simplify the graph into fewer vertices with every move when possible.
I considered using the A* algorithm, but I haven’t had a chance to fully explore that option. Instead, I decided to try a simple greedy Best First Search, which is an improved version of Breadth First Search that allows me to specify certain rules that help me choose which nodes of the graph to dequeue. Each node of the graph is given a heuristic property, and I update this property as I generate the tree. The important clue to figuring out the heuristic is this: every single move must eliminate at least one color shape in order to make progress towards the solution. Any other move is a waste of a move and thus a waste of time.
The heuristic is simple: each game state that is generated in the game tree has a heuristic property that is equal to how many fewer color shapes it has compared to the original number of color shapes at the start of the level. This is used as a way to measure how much progress each game state has (how far away it is from the starting game state, and thus how close it seems to be to the solution state). We can’t simply use this as the heuristic alone, though, because it doesn’t eliminate enough nodes from the tree to consider at a higher priority (we’d have too many game states with the same heuristic). So we need a way to break these ties in order to give priority to states in a different way. We can use the game state’s tree level to do this. If a game state is located closer to the root game state than another game state (it is on a lower level), then this is enough information for us to improve our heuristic. This way, I ensure that when I find a solution, it will be at the lowest level I’ve seen so far. Thus our heuristic for each game state will be the following:
heuristic = (original # of shapes - # of shapes removed in this game state) + (game state tree level)Let’s look at the code, which in essence turns the queue that we used in the original Breadth First Search algorithm into a priority queue:
// solveBestFirstSearch: Generates a game tree using a heuristic-based Breadth First Search to find the best solution.
1. Graph.prototype.solveBestFirstSearch = function(colors) { // colors is an array of color strings
2. this.pruneGraph(); // simplify graph before solving.
3. this.level = 0; // store the game tree level with each game state. This is the root node.
// if only one game state is present, then board is solved! in case board is passed in solved ;)
4. if (this.size() === 1) {
5. printSolution(this); // same function from original BFS code
6. return this.level;
7. }
8. const originalPrunedSize = this.size();
9. this.heuristic = originalPrunedSize;
10. var queue = [this];
11. var visited = new Set();
12. visited.add(getHash(this)); // getHash is same function from original BFS code
13. while (queue.length) {
// Get the index of the node in the queue that has the lowest heuristic
14. var lowest = 0;
15. for (var i = 0; i < queue.length; i++) {
16. if (queue[i].heuristic < queue[lowest].heuristic) {
17. lowest = i;
18. }
19. }
20. var poppedGraph = queue[lowest];
21. if (poppedGraph.size() === 1) { // check if this 'ideal' node is solved:
22. printSolution(poppedGraph);
23. return poppedGraph.level;
24. }
25. queue.splice(lowest, 1); // remove the node from the queue
26. visited.add(getHash(poppedGraph));
27. for (var v = 0; v < poppedGraph.size(); v++) { // for each vertex
28. for (var c = 0; c < colors.length; c++) { // for each color
29. const poppedVertex = poppedGraph.vertices[v];
// Make sure this node isn't the same color as the color I want to flood fill with:
30. if (colors[c] !== poppedGraph.vertexColors[poppedVertex].color) {
31. const edgesOfpoppedVertex = poppedGraph.edges[poppedVertex];
32. // Make sure we can reduce the graph by at least one color shape:
33. if (edgesOfpoppedVertex.length == 1 &&
poppedGraph.vertexColors[edgesOfpoppedVertex[0]].color == colors[c]) break;
34. var graphCopy = new Graph(poppedGraph.vertexColors, poppedGraph);
35. graphCopy.vertexColors[graphCopy.vertices[v]].color = colors[c];
36. graphCopy.level = poppedGraph.level + 1; // set game tree level
37. graphCopy.parent = poppedGraph; // set parent so we can backtrack to root node to trace solution
38. // keep track of potential solution paths:
39. graphCopy.changeMade = 'Color the shape at triangle ' + poppedVertex + ' ' + colors[c];
40. var nodesBeforePruning = graphCopy.vertices.length;
41. graphCopy.pruneGraph(); // simplify graph to reflect changes
42. var nodesAfterPruning = graphCopy.vertices.length;
43. var colorShapesRemoved = nodesBeforePruning - nodesAfterPruning;
44. var heuristic = (originalPrunedSize - colorShapesRemoved) + graphCopy.level;
45. var thisHeuristicIsBest = false; // used to see if this is the best version of this game state
46. if (!visited.has(getHash(graphCopy)) && colorShapesRemoved > 0) {
// only enqueue unique game states that have progress (at least 1 color shape eliminated)
// This the the first time we have arrived at this node,
// so it is the best (and only) version of it we've seen so far
47. thisHeuristicIsBest = true;
48. queue.push(graphCopy);
49. } else if (heuristic < (graphCopy.heuristic)) {
// We have already seen the node, but last time it had a worse heuristic
50. thisHeuristicIsBest = true;
51. }
52. if (thisHeuristicIsBest) { // if this heuristic is indeed the best for this node, use it
53. graphCopy.heuristic = heuristic; // we found an optimal (so far) path to this node.
54. }
55. }
56. }
57. }
58. }
59. return -1; // no solution found
60. };This algorithm uses the heuristic I described to determine which nodes to dequeue from the priority queue. I am also able to prune my game tree generation even more than I did in my original Breadth First Search Algorithm. When considering whether I should color a particular color shape a certain color, I can ignore the following situations:
- Trying to change the color shape to its own color (which would result in having the same number of color shapes that I started with)
- Changing the color of a color shape that is only connected to one node that is a different color (which also would result in having the same number of color shapes that I started with)
These both create wasted moves that don’t contribute to the solution, so we don’t need to consider them. This speeds up the algorithm slightly. For the example board that has 64 color shapes, this algorithm finds the best solution (6 moves) in approximately 22 seconds, compared to what would likely be hours if I had enough memory to run the original Breadth First Search algorithm on the board! Since we also keep track of each game state’s parent, when we find a solution, we can backtrack from the solved game state to the root node to get the list of moves in the solution. Here is the solution for this level:
The triangle number represents a location of the triangle on the board that matches a color shape (it is always the topmost and leftmost triangle of the color shape).
There is one important thing to note about this improved algorithm. Although the heuristic can be used to speed up the solution search for many levels, there are cases where complex levels that have a similar change in the reduction in the number of color shapes for boards with a lot of colors and color shapes will simply decompose into Breadth First Search since it will have many levels that are considered the “same” to the algorithm. In these cases, it may be possible to use an improved heuristic, but my brain isn’t smart enough to figure that out quite yet! :)
At this point, finishing up the game is pretty straightforward. We can add the number of moves necessary to solve each level to our game levels since we can now calculate that number with our solver. Then when the user runs out of moves without solving, we can end the game.
This was a very exciting project for me, one that I started two long weeks ago. It took me that much time to write the game (I would’ve finished much sooner had I not learned React literally the week before!). Most of my time was spent either trying to figure out nuances regarding React or JavaScript, generating the grid, and writing the algorithm to solve a level. I’m so relieved to be finished, and I learned a LOT about React and even more about graph theory. The most rewarding part was writing the Best First Search algorithm, which I’ve never done before. :)
I hope this was both informative and interesting!
Powered by QuickLatex


















Wow, I’m really glad I came across this article. I also enjoy Kami2, and wrote a solver for it a few months back. It is indeed a nice exercise in graph theory and search algorithms. As another commenter also pointed out, A* is indeed applicable here, for example using a heuristic that counts the number of remaining colors (minus 1).
My article, which I posted before seeing this one, is at https://cmath-school.com/blog/kami2-ai. I just added an “update” paragraph linking to yours and acknowledging the similarities.
Cheers,
Chris Olston
That’s cool! I have used the same puzzle as a tool to practice some multithreaded programming and to have some fun. I came up with the same “game tree” of yours and used the ideas from branch & bound algorithms. I tried to eliminate some nodes of the game tree if they are not promising. To do that I had to came up with a lower bound on the minimum number of remaining moves for a given graph. Then I thought that one should unite all nodes in the simplified graph including those that are most distant to each other. Then I find the diameter of the “simplified graph”. if the diameter d is odd then a lower bound would be (d-1)/2. I took some inspiration from the puzzles 55 and alike. If there are multiple connected components in the simplified graph, then this should be done for each of them and then the numbers should be summed up. Another lower bound is the remaining number of distinct colors on the simplified graph minus 1. The greater of the two would be the stronger one. Using this lower bound you can determine at any node on the game tree, if it can lead to a better solution than the one that is already found. If not just don’t do the node. This shorthens the search time. Also, following the idea from puzzle 55, a heuristic would be to start from the middle of the longest shortest path on the simplified graph. I haven’t tried this yet though.
Another interesting problem for me regarding the same puzzle is constructing the simplified graph out of the screenshot of the puzzle. The colors of the triangles on the puzzle are not solid and the triangles of the same color and the squares in the legend have some variance and there are some outliers as well. I can see that you replicated the second property but not the first one. I guess that’s the main difference in terms of appearance between your version of the puzzle and the original one. It makes the puzzle visually more appealing but at the same time harder to process. Doing it without human input is not that trivial to me. I first took some sample pixels from the triangle and averaged, and used k-means to cluster the colors, but I haven’t perfected that. For some problems I needed to correct the color of a couple nodes in the not-yet-simplified graph manually.
Thanks for writing this story, it is fun to see other people spending some decent time for such a thing to enjoy and learn at the same time.
This was very well written and enjoyable to read. Thank you!
You may have come across this paper that flood filling games with sufficient number of colors are NP-hard: https://arxiv.org/abs/1001.4420.
I haven’t dived into it but i’d guess it applies to this board layout too.
Hi Mike! That would be a fun experiment. Maybe I’ll look into that game next! :)
I’ll tell you what I’ve always wanted to figure out, a mathematical way to find optimal solutions for TrainYard. I know there is a way to model it but I just can’t figure it out.
This is a really good article, and I’ve found it extremely useful. I’m in the process of implementing a C#/WPF Kami2 Solver and have used some of the ideas here. I love the way there’s lots of Compter Science stuff as well – Graphs, BFS, DFS, etc. It must have taken a long time to create all those images, but it really helps with the explanations. Thank you for writing this :)
Wow! This is so well written that I could actually understand it! Very nice! Can you turn this in for computer class for extra credit! Lol
Mom