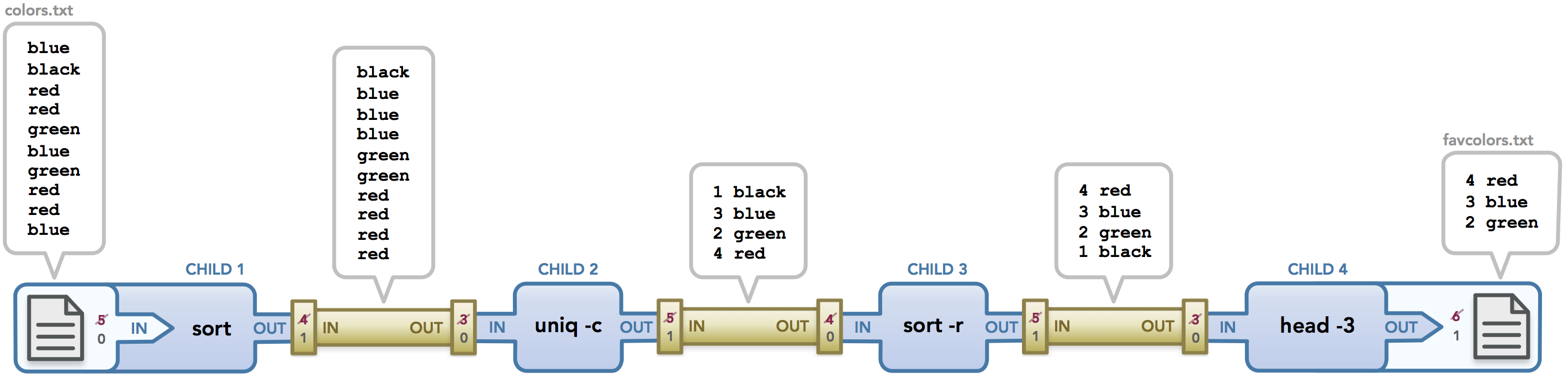
I'm currently enrolled in a systems programming class at Stanford (CS110: Principles of Computer Systems). It is the second systems class I've taken (the first was CS107 which teaches C and focuses on understanding pointers and memory management). This class focuses mainly on the inner workings of the operating system, using C and C++ to teach us concepts like process management, program execution, and handling data. While I enjoyed and quickly grasped the concepts taught in CS107, I've had a harder time understanding the material in CS110. The class itself is extremely interesting and well-taught, but my main pain point has been understanding the way processes share data and how input and output work across commands entered in the terminal. In the last few days, however, I finally found clarity when I started creating diagrams to model process behavior and the path that data takes as it travels from one command to another. I'd like to share what I've learned with you. In this post, we'll go over how Unix commands pass data to each other via pipes and input/output redirection and I'll illustrate what actually happens to the flow of data when a command is executed.
Continue reading →